曲靖事业单位职测考试题本(1月26日)

　1. 某论坛上午举办甲会议，下午举办乙会议。报名参加甲会议和乙会议的人次之和正好为520。已知甲会议共报名240人。且报名参加甲会议的人中有一半报名参加乙会议，问仅报名参加乙会议的人数约占至少报名参加2个会议之一总人数的：

　　A.30%

　　B.40%

　　C.50%

　　D.60%

　　2. 上海徐汇初三某班共有同学45名，参加学校组织的化学竞赛和计算机竞赛的选拔赛，如果化学竞赛通过的人数有30人，计算机竞赛通过的有25人，两个选拔赛都没通过的有3人，那么两个选拔赛都通过的有( )人。

　　A.7

　　B.13

　　C.15

　　D.20

　　3. 某单位员工中有45人订阅A刊，有49人订阅了B刊，有58人订阅了C刊，有16人订阅了A刊和B刊，有23人订阅了B刊和C刊，有21人订阅了A刊和C刊。有10人同时订阅了这三种刊物。该单位至少订阅一种刊物的人数是：

　　A.88

　　B.95

　　C.102

　　D.109

　　4. 某班级55名同学参加语文、数学二门课的考试。已知语文51人及格，数学48人及格，则只有语文一门课程及格的人数最多有( )人。

　　A.3

　　B.4

　　C.7

　　D.8

　　5. 某班有54名学生，共中有24名同学喜欢唱歌，有32名同学喜欢跳舞，唱歌、跳舞都不喜欢的有7名同学，那么既喜欢唱歌也喜欢跳舞的同学有多少人?

　　A.9

　　B.23

　　C.28

　　D.13
 

　　1.【答案】B

　　【解析】第一步，本题考查容斥问题，属于二集合容斥类，用画图法解题。

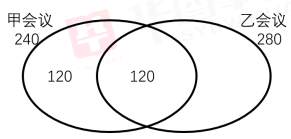
　　第二步，设报名乙会议人数为x，甲会议报名240人，两个会议均报名120人，根据总人次为520列方程，240+x=520，解得x=280，由题意可画出下图

　　第三步，仅报名参加乙会议人数=280-120=160人，至少报名参加2个会议之一总人数=240+280-120=400。仅报名参加乙会议人数占至少报名参加2个会议之一总人数=160÷400=40%。

　　因此，选择B选项。

　　2.【答案】B

　　【解析】第一步，本题考查容斥问题，属于二集合容斥类。

　　第二步，设两个选拔都通过的有x人。根据二集合容斥标准型公式可得，30+25-x=45-3，解得x=13。故两个选拔赛都通过的有13人。

　　因此，选择B选项。

　　3.【答案】C

　　【解析】第一步，本题考查容斥问题，属于三集合容斥类。

　　第二步，根据三集合标准型核心公式：总数-都不满足的=集合A+集合B+集合C-A∩B-B∩C-A∩C+都满足的，可知，至少订阅一种刊物的人数为：45+49+58-16-23-21+10=102(人)。

　　因此，选择C选项。

　　4.【答案】C

　　【解析】解法一：

　　第一步，本题考查容斥原理，属于二集合容斥类。

　　第二步，语文不及格有55-51=4人，数学不及格有55-48=7人，则数学和语文都及格至少有55-(4+7)=44人，只有语文一门及格的最多有51-44=7人。

　　因此，选择C选项。

　　解法二：

　　第一步，本题考查容斥原理，属于二集合容斥类。

　　第二步，只有语文一门课程及格的人数=语文及格人数-数学和语文都及格人数，要求“只有语文一门课程及格的人数”的最大值，则先求“数学和语文都及格人数”的最小值。数学和语文都及格人数=51+48-55+数学和语文都不及格人数=44+数学和语文都不及格人数，令数学和语文都不及格人数=0，此时得数学和语文都及格人数取得最小值为44人，故只有语文一门课程及格的人数最多有51-44=7(人)。

　　因此，选择C选项。

　　【拓展】两集合标准型核心公式：总数-都不满足的=集合A+集合B-都满足的

　　5.【答案】A

　　【解析】第一步，本题考查容斥问题，属于二集合容斥类。

　　第二步，设既喜欢唱歌也喜欢跳舞的同学有x人，根据二集合容斥公式，54-7=24+32-x。解得x=9。

　　因此，选择A选项。
 

（编辑：admin）